Project Portfolio

MSc DISSERTATION

Us versus Them. This dissertation explores the formation of friendly and opposing parties on signed networks. We outline what it means for a graph of relationships to be balanced, motivated by concepts in social psychology. We compare existing models for how such relationships evolve, where the governing differential equations are interpreted as the effects of gossiping and communication, and explore the structure of the resulting social networks. Opinions under such dynamics tend to diverge in magnitude, hence we investigate known models that bound the opinions to a prescribed range. We then present new convergence proofs and prove the stability of different social states under such models.

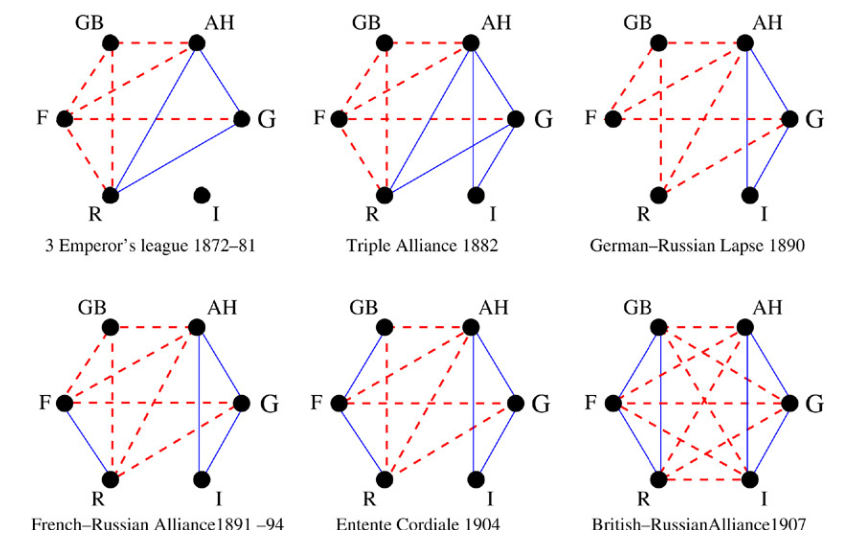
We outline a novel control model, which nudges the opinions towards a social configuration prescribed by a state vector, termed the diplomatic target. We apply this model to two case studies: the alliances and enmity of nations in the period preceding WWI (shown); and Zachary’s karate club study, a well-known example of group fission in network theory. Our model correctly classifies the final allegiances in both cases. We also introduce and investigate the bifurcating dynamics on two coupled graphs, known as a multiplex graph. We interpret different layers of the multiplex graph as different arenas of social interaction. We find that coupled graphs can tend toward separate states of balance and still be stable under the presented dynamics. From a social perspective, we argue that this accounts for cognitive dissonance: individuals may subscribe to different ideologies depending on the topic, or countries might choose different sides depending on the diplomatic context.

Keywords Networks, Heider's Social Balance Theory, Stability and Bifurcations of Dynamical Systems, Control Theory

• PDF

IEEE PUBLICATION

A patient is undergoing radiation treatment for thyroid cancer. Accurate estimation of the radiation dose delivered to the patient is key in determining the effectiveness of therapy, patient prognosis, and decisions on further treatment. But if the radiation is absorbed by the thyroid itself, we can't measure it directly. And if other patient measurements are sparse and uncertain, then how can we more accurately estimate the dose the patient actually receives? The answer: we use data from other patients.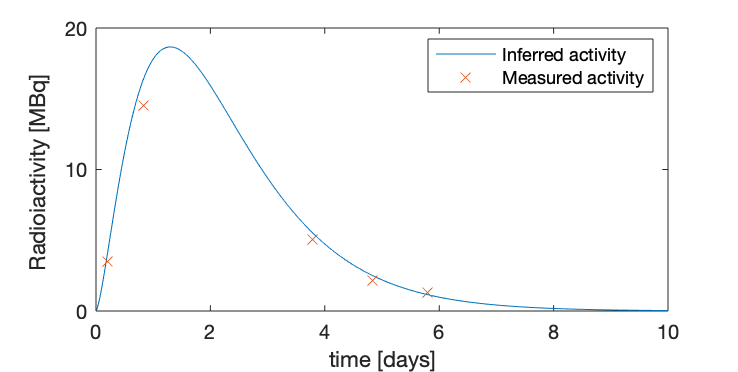

When we process new data or knowledge, our beliefs can change, and Bayesian statistics provides the tools to model such learning. Here, our beliefs in the radiation dose are captured by parameters dictating the shape of the inferred radioiodine uptake-clearance curve (shown in blue).
To supplement knowledge from the patient's own measurements (in red), we can use knowledge gathered from past patient data. We propose that this knowledge may be selectively chosen, i.e. identifying a subgroup of similar past records, in order to improve the estimates of the radiation dose delivered to a specific patient.
The selected knowledge is transferred by forming a parameter-based radioiodine activity predictor from the subgroup data. We use this to 'interpolate the gaps' in the target patient's data. Our proposed method is significant in that it can be applied to other transfer learning applications where inhomogeneous parameter knowledge is available in the source feature space.

Keywords Bioinformatics, Decision Support Systems, Nuclear Medicine, Bayesian Transfer Learning, Gaussian Mixture Modelling

• View on IEEE Xplore
• PDF

My interests lie in cross-disciplinary quantitative research, applying mathematical and engineering tools to medicine, sociology, finance, and biology. Some of my projects and publications involve Bayesian machine-learning approaches to improve radiation dose inference in nuclear medicine, dynamic network theory applied to study evolving relations between social groups, and computational analysis of biological pattern formation.
I have recently received an MSc in Mathematical Modelling and Scientific Computing from the University of Oxford. I also have a BAI (Sch.) in Electronic and Computer Engineering from Trinity College Dublin.